在R中进行统计建模时,分类或名称数据的首选表示方法是因子(factor),这是一种只能取有限个不同值的变量;在内部,因子以整数向量的形式存储,并附带一组文本标签。在第8.4.1节中,我们介绍了特征工程方法,用于将定性或名称数据编码或转换为更适合大多数模型算法的表示形式。我们讨论了如何将一个分类变量(例如Ames住房数据中的Bldg_Type,其水平包括OneFam、TwoFmCon、Duplex、Twnhs和TwnhsE)转换为一组虚拟变量或指示变量,如 Table 1 所示。
许多模型实现都需要将分类数据转换为数值表示形式。附录A列出了适用于不同模型的推荐预处理技术表;请注意,表中许多模型均要求对所有预测变量进行数值编码。
然而,对于一些实际的数据集,直接使用虚拟变量并不适用。这种情况通常是因为类别数量过多,或者在预测时出现了新类别。本章将探讨更复杂的分类预测变量编码方法,以解决这些问题。这些方法可通过 tidymodels 的 recipe 步骤,在embed 和textrecipes 包中获得。
Is an Encoding Necessary?
少数模型,例如基于树或规则的模型,能够原生处理分类数据,无需对这类特征进行编码或转换。例如,基于树的模型可直接将Bldg_Type这样的变量划分为若干个因子水平组——比如,将OneFam单独归为一组,而Duplex和Twnhs则合并为另一组。此外,朴素贝叶斯模型也是另一种典型例子:其模型结构本身就能自然地应对分类变量,具体而言,会在每个水平内分别计算概率分布,如针对数据集中所有不同类型的Bldg_Type。
这些能够原生处理分类特征的模型,同样也能应对数值型、连续型特征,因此对这类变量的转换或编码变得可有可无。但这是否会在某种程度上帮助提升模型性能或缩短训练时间呢?通常情况下,并非如此——正如 M. Kuhn 和 Johnson(2020年)书中第5.7节所指出的,使用未经转换的因子变量与针对相同特征转换为虚拟变量后进行对比时,基准数据集的表现显示:采用虚拟编码方式不仅未显著改善模型性能,反而常常需要更长的训练时间。
我们建议,在模型允许的情况下,优先使用未经过转换的分类变量;需要注意的是,对于这类模型,更复杂的编码方式通常并不会带来更好的性能。
Encoding Ordinal Predictors
有时,定性列可以进行排序,例如“低”、“中”和“高”。在 base R 中,默认的编码策略是创建新的数值列,这些列是数据的多项式展开。对于具有五个有序值的列——如 Table 2 所示的例子——因子列会被替换为线性、二次、三次和四次项的列:
虽然这种做法并非毫无道理,但人们通常并不觉得它有用。例如,用一个11次多项式来编码一年中各个月份的顺序型因子,可能并不是最有效的方法。相反,不妨尝试使用与有序因子相关的recipe步骤,比如step_unorder() step_ordinalscore()
Using the Outcome for Encoding Predictors
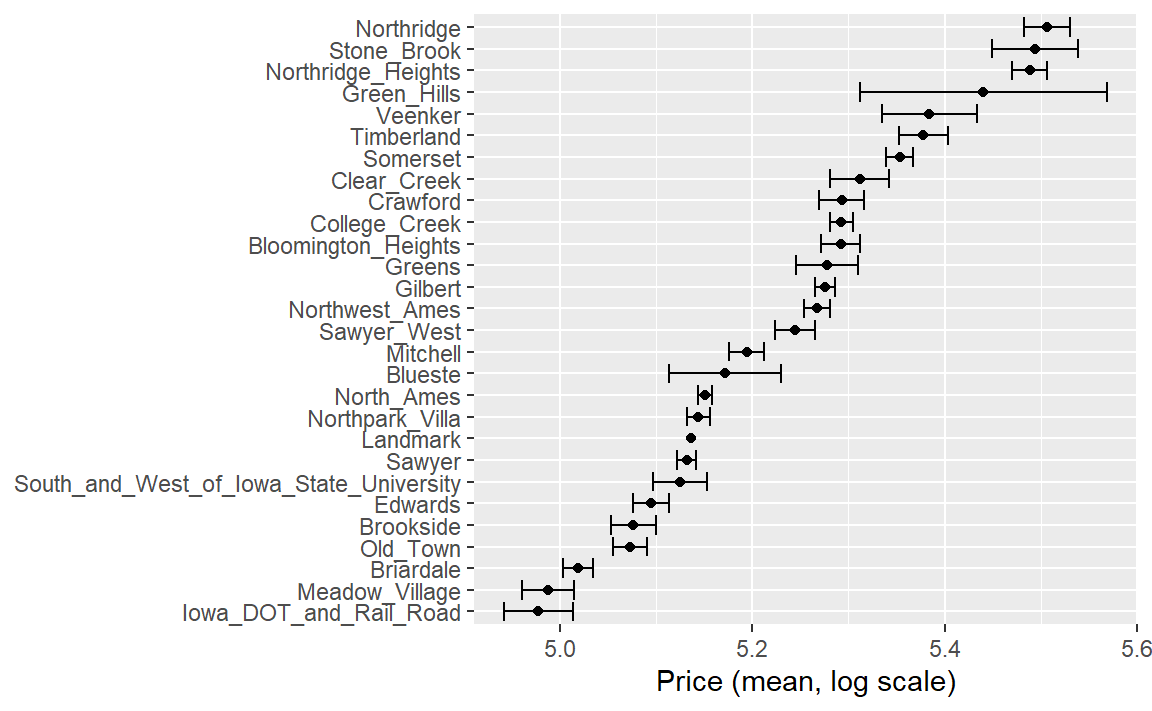
除了虚拟变量或指示变量之外,还有多种更复杂的编码方式可供选择。其中一种方法称为效应编码(effect encoding)或似然编码(likelihood encoding),它用单个数值列取代了原有的分类变量,该数值列用于衡量这些数据的效应(Micci-Barreca 2001;Zumel 和 Mount 2019)。例如,在Ames住宅数据中,针对街区这一预测变量,我们可以计算每个街区的平均或中位数销售价格(如 Figure 1 所示),并用这些均值替换原始数据值:
library ( tidymodels ) #> ── Attaching packages ─────────────────────────────────── tidymodels 1.4.1 ── #> ✔ broom 1.0.9 ✔ recipes 1.3.1 #> ✔ dials 1.4.2 ✔ rsample 1.3.1 #> ✔ dplyr 1.1.4 ✔ tailor 0.1.0 #> ✔ ggplot2 3.5.2 ✔ tidyr 1.3.1 #> ✔ infer 1.0.9 ✔ tune 2.0.0 #> ✔ modeldata 1.5.1 ✔ workflows 1.3.0 #> ✔ parsnip 1.3.3 ✔ workflowsets 1.1.1 #> ✔ purrr 1.1.0 ✔ yardstick 1.3.2 #> ── Conflicts ────────────────────────────────────── tidymodels_conflicts() ── #> ✖ purrr::discard() masks scales::discard() #> ✖ dplyr::filter() masks stats::filter() #> ✖ dplyr::lag() masks stats::lag() #> ✖ recipes::step() masks stats::step() data ( ames ) ames <- mutate ( ames , Sale_Price = log10 ( Sale_Price ) ) set.seed ( 502 ) ames_split <- initial_split ( ames , prop = 0.80 , strata = Sale_Price ) ames_train <- training ( ames_split ) ames_train %>% group_by ( Neighborhood ) %>%
summarize (
mean = mean ( Sale_Price ) ,
std_err = sd ( Sale_Price ) / sqrt ( length ( Sale_Price ) )
) %>%
ggplot ( aes ( y = reorder ( Neighborhood , mean ) , x = mean ) ) +
geom_point ( ) +
geom_errorbar ( aes ( xmin = mean - 1.64 * std_err , xmax = mean + 1.64 * std_err ) ) +
labs ( y = NULL , x = "Price (mean, log scale)" )
当你的分类变量具有大量水平时,这种效应编码方法效果尤为出色。在tidymodels中,embed包提供了多种用于不同效应编码的recipe步骤函数,例如step_lencode_glm() step_lencode_mixed() step_lencode_bayes() step_lencode_glm() vars()指明结果变量:
library ( embed ) ames_glm <- recipe ( Sale_Price ~ Neighborhood + Gr_Liv_Area + Year_Built + Bldg_Type +
Latitude + Longitude , data = ames_train ) %>%
step_log ( Gr_Liv_Area , base = 10 ) %>%
step_lencode_glm ( Neighborhood , outcome = vars ( Sale_Price ) ) %>%
step_dummy ( all_nominal_predictors ( ) ) %>%
step_interact ( ~ Gr_Liv_Area : starts_with ( "Bldg_Type_" ) ) %>%
step_ns ( Latitude , Longitude , deg_free = 20 )
ames_glm #> #> ── Recipe ─────────────────────────────────────────────────────────────────── #> #> ── Inputs #> Number of variables by role #> outcome: 1 #> predictor: 6 #> #> ── Operations #> • Log transformation on: Gr_Liv_Area #> • Linear embedding for factors via GLM for: Neighborhood #> • Dummy variables from: all_nominal_predictors() #> • Interactions with: Gr_Liv_Area:starts_with("Bldg_Type_") #> • Natural splines on: Latitude Longitude
正如第16.4节所详述,我们可以使用训练数据对recipe进行prep() tidy()
glm_estimates <- prep ( ames_glm ) %>%
tidy ( number = 2 )
glm_estimates #> # A tibble: 29 × 4 #> level value terms id #> <chr> <dbl> <chr> <chr> #> 1 North_Ames 5.15 Neighborhood lencode_glm_yj20u #> 2 College_Creek 5.29 Neighborhood lencode_glm_yj20u #> 3 Old_Town 5.07 Neighborhood lencode_glm_yj20u #> 4 Edwards 5.09 Neighborhood lencode_glm_yj20u #> 5 Somerset 5.35 Neighborhood lencode_glm_yj20u #> 6 Northridge_Heights 5.49 Neighborhood lencode_glm_yj20u #> # ℹ 23 more rows
当我们使用通过这种方法创建的全新编码的Neighborhood数值变量时,会用GLM模型中对Sale_Price的估计值来替换原始水平(例如North_Ames)。
像这种效应编码方法,也能无缝应对数据中遇到新因子水平的情况。当我们在缺乏特定小区信息时,该值value正是我们从GLM模型预测出的价格:
glm_estimates %>% filter ( level == "..new" )
#> # A tibble: 1 × 4 #> level value terms id #> <chr> <dbl> <chr> <chr> #> 1 ..new 5.23 Neighborhood lencode_glm_yj20u
效应编码功能强大,但应谨慎使用。这些效应应在数据拆分后,基于训练集进行计算。这种有监督的预处理步骤需严格采用重采样方法,以避免过拟合(参见第10章)。
当你为分类变量创建效应编码时,实际上是在你的实际模型内部叠加了一个小型模型。效应编码存在过拟合的风险,这正是第7章中所阐述的:特征工程必须被视为模型流程的一部分;同时,特征工程也应与模型参数一起,在重采样过程中一并进行估计。
Effect encodings with partial pooling
使用step_lencode_glm()
ames_mixed <- recipe ( Sale_Price ~ Neighborhood + Gr_Liv_Area + Year_Built + Bldg_Type +
Latitude + Longitude , data = ames_train ) %>%
step_log ( Gr_Liv_Area , base = 10 ) %>%
step_lencode_mixed ( Neighborhood , outcome = vars ( Sale_Price ) ) %>%
step_dummy ( all_nominal_predictors ( ) ) %>%
step_interact ( ~ Gr_Liv_Area : starts_with ( "Bldg_Type_" ) ) %>%
step_ns ( Latitude , Longitude , deg_free = 20 )
ames_mixed #> #> ── Recipe ─────────────────────────────────────────────────────────────────── #> #> ── Inputs #> Number of variables by role #> outcome: 1 #> predictor: 6 #> #> ── Operations #> • Log transformation on: Gr_Liv_Area #> • Linear embedding for factors via mixed effects for: Neighborhood #> • Dummy variables from: all_nominal_predictors() #> • Interactions with: Gr_Liv_Area:starts_with("Bldg_Type_") #> • Natural splines on: Latitude Longitude
让我们对这个recipe对象进行prep() tidy()
mixed_estimates <- prep ( ames_mixed ) %>%
tidy ( number = 2 )
mixed_estimates #> # A tibble: 29 × 4 #> level value terms id #> <chr> <dbl> <chr> <chr> #> 1 North_Ames 5.15 Neighborhood lencode_mixed_AmBz1 #> 2 College_Creek 5.29 Neighborhood lencode_mixed_AmBz1 #> 3 Old_Town 5.07 Neighborhood lencode_mixed_AmBz1 #> 4 Edwards 5.10 Neighborhood lencode_mixed_AmBz1 #> 5 Somerset 5.35 Neighborhood lencode_mixed_AmBz1 #> 6 Northridge_Heights 5.49 Neighborhood lencode_mixed_AmBz1 #> # ℹ 23 more rows
随后,新等级的编码值与GLM几乎相同:
mixed_estimates %>% filter ( level == "..new" )
#> # A tibble: 1 × 4 #> level value terms id #> <chr> <dbl> <chr> <chr> #> 1 ..new 5.23 Neighborhood lencode_mixed_AmBz1
你可以使用完全贝叶斯层次模型来以相同的方式对效应进行建模,方法是调用step_lencode_bayes()
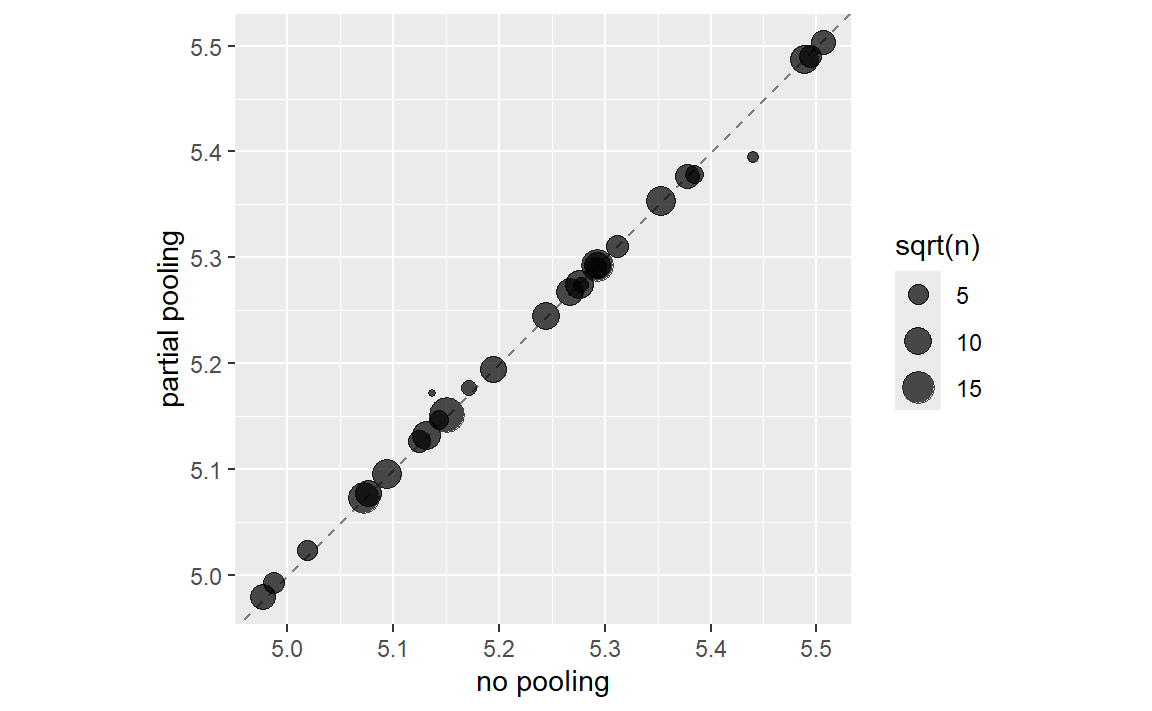
让我们在 Figure 2 中通过可视化方式比较部分聚合与无聚合的效果:
glm_estimates %>% rename ( `no pooling` = value ) %>%
left_join (
mixed_estimates %>%
rename ( `partial pooling` = value ) ,
by = "level"
) %>%
left_join (
ames_train %>%
count ( Neighborhood ) %>%
mutate ( level = as.character ( Neighborhood ) )
) %>%
ggplot ( aes ( `no pooling` , `partial pooling` , size = sqrt ( n ) ) ) +
geom_abline ( color = "gray50" , lty = 2 ) +
geom_point ( alpha = 0.7 ) +
coord_fixed ( )
#> Joining with `by = join_by(level)` #> Warning: Removed 1 row containing missing values or values outside the scale range #> (`geom_point()`).
请注意,如 Figure 2 所示,当我们比较整体聚合与完全不聚合时,大多数关于邻里效应的估计值基本一致。然而,那些房屋数量最少的社区,其效应估计值已被拉向(向上或向下)平均效应水平。这是因为采用整体聚合方法时,我们对这些社区房价的证据相对较少,因而会将效应估计值向均值靠拢。
Feature Hashing
传统虚拟变量如第8.4.1节所述,要求必须已知所有可能的类别,才能构建出完整的数值特征集。而特征哈希方法(Weinberger等,2009)同样会创建虚拟变量,但仅根据类别值将其分配到预定义的虚拟变量池中。让我们再次查看Ames数据集中的Neighborhood字段,并使用rlang::hash()
library ( rlang ) #> #> Attaching package: 'rlang' #> The following objects are masked from 'package:purrr': #> #> %@%, flatten, flatten_chr, flatten_dbl, flatten_int, #> flatten_lgl, flatten_raw, invoke, splice ames_hashed <- ames_train %>%
mutate ( Hash = map_chr ( Neighborhood , hash ) )
ames_hashed %>% select ( Neighborhood , Hash )
#> # A tibble: 2,342 × 2 #> Neighborhood Hash #> <fct> <chr> #> 1 North_Ames 076543f71313e522efe157944169d919 #> 2 North_Ames 076543f71313e522efe157944169d919 #> 3 Briardale b598bec306983e3e68a3118952df8cf0 #> 4 Briardale b598bec306983e3e68a3118952df8cf0 #> 5 Northpark_Villa 6af95b5db968bf393e78188a81e0e1e4 #> 6 Northpark_Villa 6af95b5db968bf393e78188a81e0e1e4 #> # ℹ 2,336 more rows
如果我们把“Briardale”输入这个哈希函数,每次都会得到相同的输出。在这种情况下,这些街区被称为“keys”,而输出结果则称为“hashes”。哈希函数将大小可变的输入映射为固定大小的输出。哈希函数广泛应用于密码学和数据库领域。
rlang::hash() 2^128种可能的哈希值。这对于某些应用来说非常理想,但并不适用于高基数变量(即具有大量水平的变量)的特征哈希。在特征哈希中,可能的哈希数量是一个超参数,由模型开发者通过计算整数哈希值的模来设定。例如,我们可以通过 Hash %% 16 获得16种可能的哈希值:
ames_hashed %>% ## first make a smaller hash for integers that R can handle
mutate (
Hash = strtoi ( substr ( Hash , 26 , 32 ) , base = 16L ) ,
## now take the modulo
Hash = Hash %% 16
) %>%
select ( Neighborhood , Hash )
#> # A tibble: 2,342 × 2 #> Neighborhood Hash #> <fct> <dbl> #> 1 North_Ames 9 #> 2 North_Ames 9 #> 3 Briardale 0 #> 4 Briardale 0 #> 5 Northpark_Villa 4 #> 6 Northpark_Villa 4 #> # ℹ 2,336 more rows
现在,我们不再使用原始数据中的28个街区,也不再处理数量极其庞大的原始哈希值,而是仅保留了16个哈希值。这种方法速度非常快,且内存效率高,尤其在可能类别数量众多时,不失为一种不错的策略。
特征哈希法不仅适用于文本数据,也适用于高基数的类别型数据。有关使用文本预测变量的案例研究演示,请参阅Hvitfeldt和Silge(2021)第6.7节。
我们可以使用来自textrecipes 包的recipe步骤来实现特征哈希:
library ( textrecipes ) ames_hash <- recipe ( Sale_Price ~ Neighborhood + Gr_Liv_Area + Year_Built + Bldg_Type +
Latitude + Longitude , data = ames_train ) %>%
step_log ( Gr_Liv_Area , base = 10 ) %>%
step_dummy_hash ( Neighborhood , signed = FALSE , num_terms = 16L ) %>%
step_dummy ( all_nominal_predictors ( ) ) %>%
step_interact ( ~ Gr_Liv_Area : starts_with ( "Bldg_Type_" ) ) %>%
step_ns ( Latitude , Longitude , deg_free = 20 )
#> 1 package (text2vec) is needed for this step but is not installed. #> To install run: `install.packages("text2vec")` ames_hash #> #> ── Recipe ─────────────────────────────────────────────────────────────────── #> #> ── Inputs #> Number of variables by role #> outcome: 1 #> predictor: 6 #> #> ── Operations #> • Log transformation on: Gr_Liv_Area #> • Feature hashing with: Neighborhood #> • Dummy variables from: all_nominal_predictors() #> • Interactions with: Gr_Liv_Area:starts_with("Bldg_Type_") #> • Natural splines on: Latitude Longitude
特征哈希法速度快、效率高,但也存在一些缺点。例如,不同的类别值常常会被映射到同一个哈希值上,这被称为冲突或别名现象。那么,在Ames的各个社区中,这种情况究竟有多频繁呢?Table 3 展示了每个哈希值对应的社区数量分布情况。
映射到每个哈希值的街区数量介于零到四之间。所有大于一的哈希值均属于哈希冲突的实例。
使用特征哈希时,有哪些需要考虑的事项?
特征哈希无法直接解释,因为哈希函数不可逆。我们无法从哈希值推断出输入的类别级别,也无法判断是否发生了冲突。
哈希值的数量是这种预处理技术的一个调优参数,您应尝试多个数值,以确定哪种设置最适合您的特定建模方法。哈希值数量较少时会导致更多冲突,但若数量过高,可能并不会比您原本高基数变量的表现更好。
特征哈希能够在预测时处理新的类别级别,因为它不依赖于预先确定的虚拟变量。
你可以通过设置signed = TRUE,来减少有符号哈希中的哈希冲突。这样,哈希值将从原来的 1 扩展为根据哈希符号决定的 +1 或 -1。
很可能会有一些哈希列包含全零值,正如我们在本例中所看到的。我们建议使用step_zv()
More Encoding Options
还有更多选项可用于将因子转换为数值表示。
我们可以构建一套完整的实体嵌入(entity embeddings,Guo 和 Berkhahn,2016),将具有多个类别的分类变量转换为一组低维向量。这种方法尤其适用于类别数量众多的名称变量——其类别数远超我们在Ames市社区示例中所使用的数量。实体嵌入的概念源自用于从文本数据中创建词嵌入的方法。更多关于词嵌入的内容,请参阅Hvitfeldt和Silge(2021)第5章。
可以通过使用embed包中的step_embed()
另一种可用于处理二元结果的选项是,根据类别水平与二元结果的关联程度对其进行转换。这种基于证据权重(WoE)的转换方法(Good,1985)利用“贝叶斯因子”的对数(即后验比值与先验比值之比),并建立一个字典,将每个类别水平映射到相应的WoE值。WoE编码可通过embed中的step_woe()
Chapter Summary
在本章中,你学习了如何使用预处理方案对分类预测变量进行编码。将分类变量转换为数值表示的最直接方法是根据其水平创建虚拟变量,但当变量的基数较高(水平数量过多)或在预测时可能遇到新值(出现新水平)时,这种方法的效果并不理想。在这种情况下,一种选择是采用效应编码,这是一种基于监督的学习编码方法,它会利用目标变量的信息。效应编码既可以单独学习,也可以通过类别聚合的方式进行学习。此外,还有一种方法是使用哈希函数,将类别映射到一组更小的新虚拟变量上。特征哈希法速度快、内存占用低。其他可选方法还包括:通过神经网络学习得到的实体嵌入,以及证据权重转换法。
大多数模型算法都需要对分类变量进行某种形式的转换或编码。而少数模型,包括基于树和规则的模型,则能直接处理分类变量,无需此类编码。