在1.2节中,我们概述了模型的分类法,并指出大多数模型可归类为描述性、推理性及/或预测性。
本书的大部分章节都从预测值的准确性角度出发,探讨了模型的相关问题——这一特性对所有类型的模型都很重要,尤其在预测模型中尤为关键。而推断性模型的构建,通常不仅为了实现预测功能,还旨在对模型中的某些要素(如系数值或其他参数)做出推论或判断。这些推断结果常被用来解答一些事先设定好的问题或验证相关假设。相比之下,在预测模型中,我们通常借助对预留数据的预测结果来评估或衡量模型的质量;而在推断性模型中,则更注重检验建模前预先设定的概率值或结构假设是否合理。
例如,在普通的线性回归中,通常假设残差彼此独立,并且服从均值为零、方差恒定的正态分布。尽管你可能具备科学或领域知识,能够为模型分析中的这一假设提供支持,但实际操作中,通常仍需检查拟合模型所得的残差,以判断该假设是否合理。因此,判断模型假设是否满足的方法,并不像单纯查看预留数据的预测结果那样简单——尽管它同样非常有用。
本章我们将使用p值,然而 tidymodels 框架更倾向于置信区间而非p值,作为衡量支持备择假设证据的方法。正如第11.4节先前所展示的,从解释的便捷性来看,贝叶斯方法通常优于p值和置信区间(但其计算成本可能更高)。近年来,人们越来越倾向于摒弃p值,转而采用其他方法(Wasserstein 和 Lazar,2016)。更多相关信息及讨论,请参阅《The American Statistician》第73卷。
在本章中,我们介绍如何使用tidymodels来拟合和评估推断模型。在某些情况下,tidymodels框架可以帮助用户处理模型生成的对象;而在另一些情况下,它则能用于评估特定模型的质量。
Inference for Count Data
我们以一个计数数据为例,来了解如何使用tidymodels包进行推断性建模。我们将使用来自pscl包的生物化学发表论文数据。这些数据包含915名生物化学博士毕业生的信息,旨在解释影响他们学术产出的因素(以三年内发表的文章数量或计数衡量)。预测变量包括毕业生的性别、婚姻状况、毕业生至少5岁孩子的数量、所在院系的声望,以及其导师同期发表的文章数量。数据记录的是1956年至1963年间完成学业的生物化学博士,但由于信息完整性问题,这一样本在一定程度上存在偏差,并不能完全代表该时期所有生物化学博士的情况。
回想一下,在第19章中,我们曾提出过这样一个问题:“我们的模型是否适用于预测某个特定的数据点?” 明确推断分析所适用的范围至关重要。对于示例数据而言,研究结果很可能适用于数据收集时段前后授予的生物化学博士学位。但它们是否也适用于其他类型的化学博士(例如药物化学等)呢?在进行推断分析时,这些问题不仅需要认真探讨,更应详细记录下来。
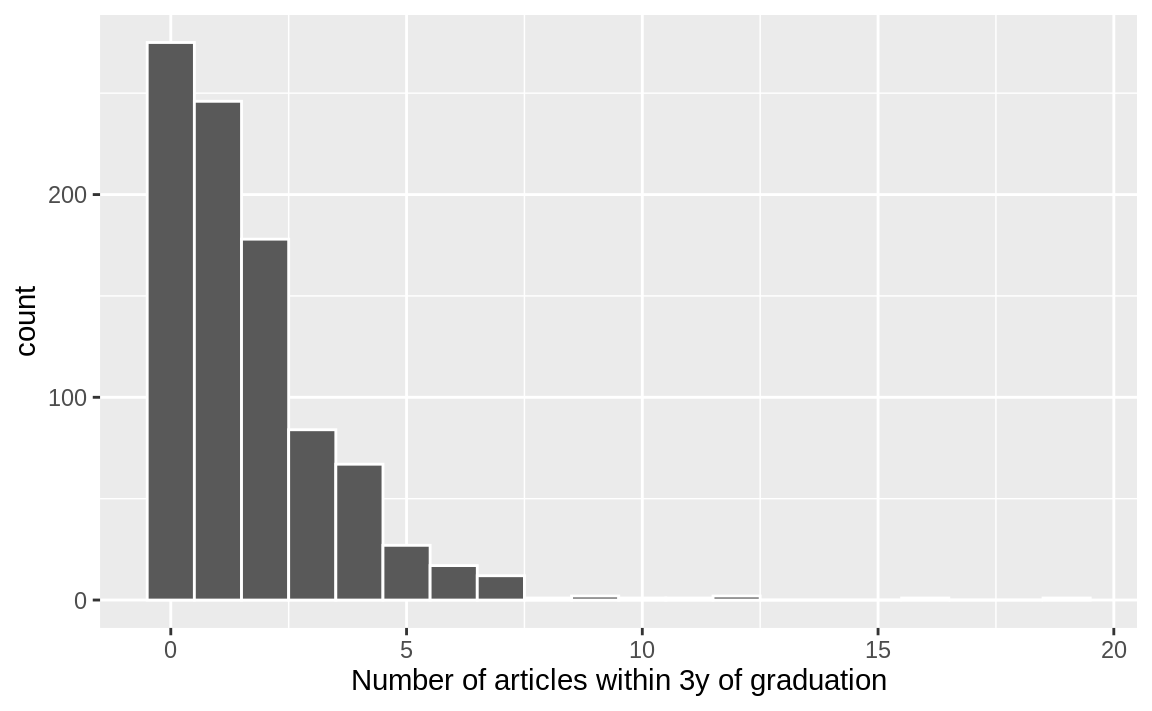
Figure 1 所示数据的图表表明,许多毕业生在此期间未发表任何文章,且结果呈现右偏分布:
library ( tidymodels ) #> ── Attaching packages ─────────────────────────────────── tidymodels 1.4.1 ── #> ✔ broom 1.0.11 ✔ recipes 1.3.1 #> ✔ dials 1.4.2 ✔ rsample 1.3.1 #> ✔ dplyr 1.1.4 ✔ tailor 0.1.0 #> ✔ ggplot2 4.0.1 ✔ tidyr 1.3.1 #> ✔ infer 1.0.9 ✔ tune 2.0.1 #> ✔ modeldata 1.5.1 ✔ workflows 1.3.0 #> ✔ parsnip 1.4.0 ✔ workflowsets 1.1.1 #> ✔ purrr 1.2.0 ✔ yardstick 1.3.2 #> ── Conflicts ────────────────────────────────────── tidymodels_conflicts() ── #> ✖ purrr::discard() masks scales::discard() #> ✖ dplyr::filter() masks stats::filter() #> ✖ dplyr::lag() masks stats::lag() #> ✖ recipes::step() masks stats::step() tidymodels_prefer ( ) data ( "bioChemists" , package = "pscl" ) ggplot ( bioChemists , aes ( x = art ) ) + geom_histogram ( binwidth = 1 , color = "white" ) +
labs ( x = "Number of articles within 3y of graduation" )
由于结果数据是计数,最常见的分布假设是:该结果服从泊松分布。本章将利用这些数据进行多种类型的分析。
Comparisons with Two-Sample Tests
我们可以从假设检验开始。原作者使用这套生物化学出版数据集的目的是,确定男性与女性之间的出版物是否存在差异(Long, 1992)。研究数据显示:
bioChemists %>% group_by ( fem ) %>%
summarize ( counts = sum ( art ) , n = length ( art ) )
#> # A tibble: 2 × 3 #> fem counts n #> <fct> <int> <int> #> 1 Men 930 494 #> 2 Women 619 421
尽管数据中男性人数更多,但男性的发表数量也明显更多。分析这些数据最简单的方法,是使用stats包中的poisson.test()
对于我们的应用,比较两性之间的假设如下,其中\(\lambda\) 值为同期的出版速率。
\[
\begin{align}
H_0&: \lambda_m = \lambda_f \notag \\
H_a&: \lambda_m \ne \lambda_f \notag
\end{align}
\]
该假设的一个基本应用是:
poisson.test ( c ( 930 , 619 ) , T = 3 ) #> #> Comparison of Poisson rates #> #> data: c(930, 619) time base: 3 #> count1 = 930, expected count1 = 774.5, p-value = 2.727e-15 #> alternative hypothesis: true rate ratio is not equal to 1 #> 95 percent confidence interval: #> 1.355716 1.665905 #> sample estimates: #> rate ratio #> 1.502423
该函数报告了发表率比值的p值及置信区间。结果显示,观察到的差异显著大于实验误差,支持备择假设 \(H_a\) 。
使用此函数的一个问题在于,结果会以htest对象的形式返回。尽管这种对象具有明确的结构,但要将其用于后续操作(如报告或可视化)时,可能会比较困难。而tidymodels为推断模型提供的最有力工具,正是broom包中的tidy() tidy()
poisson.test ( c ( 930 , 619 ) , T = 3 ) %>% tidy ( )
#> # A tibble: 1 × 8 #> estimate statistic p.value parameter conf.low conf.high method #> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> #> 1 1.50 930 2.73e-15 774. 1.36 1.67 Comparison of Poi… #> # ℹ 1 more variable: alternative <chr>
broom 与broom.mixed 包提供了150多种tidy()
尽管泊松分布是合理的,我们或许还希望在减少对分布假设依赖的情况下进行评估。两种可能有所帮助的方法是自助法和置换检验(Davison 和 Hinkley,1997)。
infer 包是 tidymodels 框架的一部分,它是一个功能强大且直观的假设检验工具(Ismay 和 Kim 2021)。其语法简洁明了,专为非统计专业人士设计。
首先,我们使用specify() calculate()
通过infer包,我们指定结果和协变量,然后说明感兴趣的统计量:
library ( infer ) observed <- bioChemists %>%
specify ( art ~ fem ) %>%
calculate ( stat = "diff in means" , order = c ( "Men" , "Women" ) )
observed #> Response: art (numeric) #> Explanatory: fem (factor) #> # A tibble: 1 × 1 #> stat #> <dbl> #> 1 0.412
从这里,我们通过generate()
set.seed ( 2101 ) bootstrapped <- bioChemists %>%
specify ( art ~ fem ) %>%
generate ( reps = 2000 , type = "bootstrap" ) %>%
calculate ( stat = "diff in means" , order = c ( "Men" , "Women" ) )
bootstrapped #> Response: art (numeric) #> Explanatory: fem (factor) #> # A tibble: 2,000 × 2 #> replicate stat #> <int> <dbl> #> 1 1 0.467 #> 2 2 0.107 #> 3 3 0.467 #> 4 4 0.308 #> 5 5 0.369 #> 6 6 0.428 #> # ℹ 1,994 more rows
百分位区间通过以下方式计算:
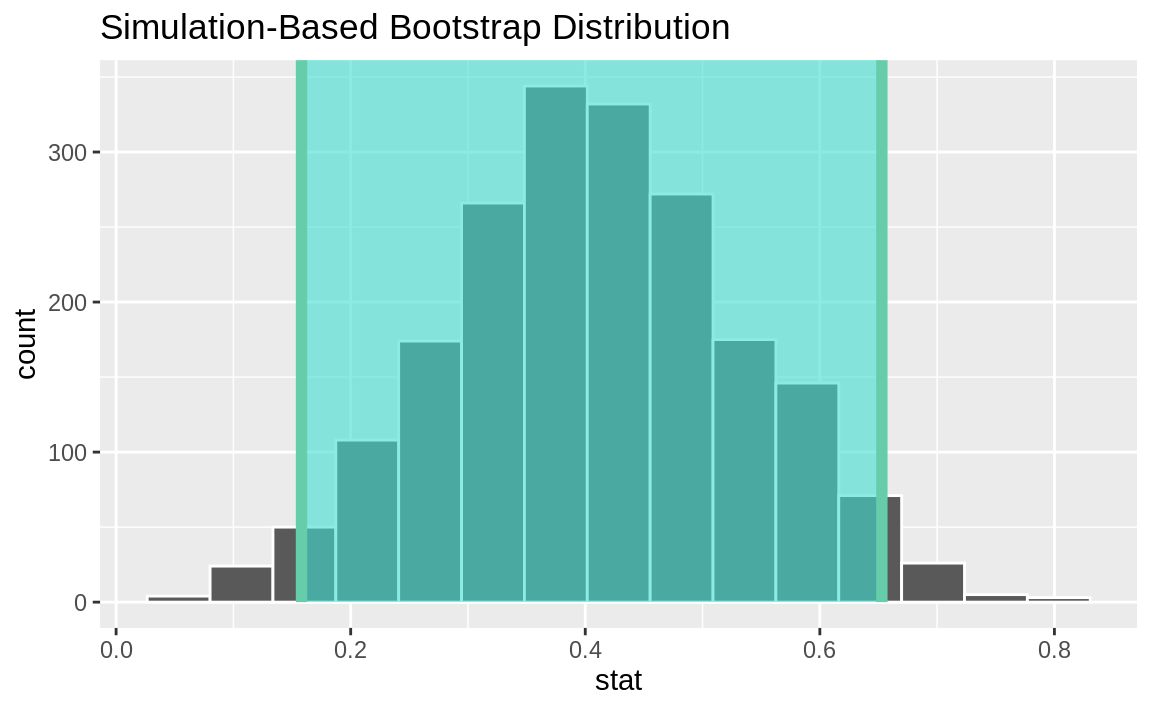
percentile_ci <- get_ci ( bootstrapped ) percentile_ci #> # A tibble: 1 × 2 #> lower_ci upper_ci #> <dbl> <dbl> #> 1 0.158 0.653
infer 包提供了一个高级 API,用于展示分析结果,如 Figure 2 所示。
由于 Figure 2 中所显示的区间不包含零,这些结果表明,男性发表的文章数量多于女性。
如果我们需要一个p值,infer 包可以通过排列检验来计算该值,具体代码如下。其语法与我们之前使用的自助法代码非常相似。我们只需添加一个hypothesize() generate()
set.seed ( 2102 ) permuted <- bioChemists %>%
specify ( art ~ fem ) %>%
hypothesize ( null = "independence" ) %>%
generate ( reps = 2000 , type = "permute" ) %>%
calculate ( stat = "diff in means" , order = c ( "Men" , "Women" ) )
permuted #> Response: art (numeric) #> Explanatory: fem (factor) #> Null Hypothesis: independence #> # A tibble: 2,000 × 2 #> replicate stat #> <int> <dbl> #> 1 1 0.201 #> 2 2 -0.133 #> 3 3 0.109 #> 4 4 -0.195 #> 5 5 -0.00128 #> 6 6 -0.102 #> # ℹ 1,994 more rows
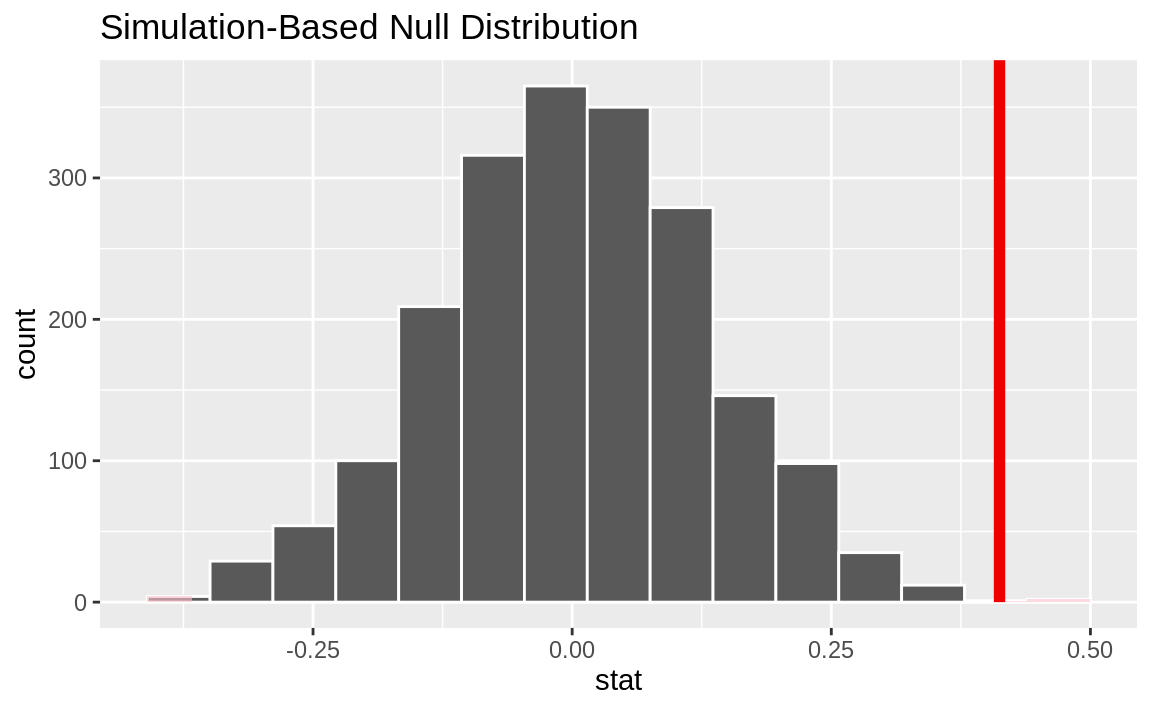
以下可视化代码也与 Bootstrap 方法非常相似。该代码生成 Figure 3 ,其中竖线表示观测值:
实际的p值是:
permuted %>% get_p_value ( obs_stat = observed , direction = "two-sided" )
#> # A tibble: 1 × 1 #> p_value #> <dbl> #> 1 0.002
Figure 3 中代表零假设的垂直线远离排列分布。这意味着,如果零假设实际上为真,那么观察到的数据至少与当前数据一样极端的可能性微乎其微。
本节中展示的两样本检验可能并非最优,因为它们未能考虑其他可能解释发表率与性别之间观测到关系的因素。让我们转向一个更复杂的模型,该模型能够纳入更多协变量。
Log-Linear Models
本章其余部分的重点将放在广义线性模型上(Dobson,1999),我们假设这些计数服从泊松分布。对于该模型,协变量/预测变量以对数线性方式进入模型,其中,\(\lambda\) 是计数的期望值:
\[
\log(\lambda) = \beta_0 + \beta_1x_1 + \ldots + \beta_px_p
\]
让我们拟合一个包含所有预测变量列的简单模型。tidymodels 中的 parsnip 扩展包——poissonreg 包,将用于拟合此模型规范:
library ( poissonreg ) # default engine is 'glm' log_lin_spec <- poisson_reg ( ) log_lin_fit <- log_lin_spec %>%
fit ( art ~ . , data = bioChemists )
log_lin_fit #> parsnip model object #> #> #> Call: stats::glm(formula = art ~ ., family = stats::poisson, data = data) #> #> Coefficients: #> (Intercept) femWomen marMarried kid5 phd #> 0.30462 -0.22459 0.15524 -0.18488 0.01282 #> ment #> 0.02554 #> #> Degrees of Freedom: 914 Total (i.e. Null); 909 Residual #> Null Deviance: 1817 #> Residual Deviance: 1634 AIC: 3314
tidy()
tidy ( log_lin_fit , conf.int = TRUE , conf.level = 0.90 ) #> # A tibble: 6 × 7 #> term estimate std.error statistic p.value conf.low conf.high #> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> #> 1 (Intercept) 0.305 0.103 2.96 3.10e- 3 0.134 0.473 #> 2 femWomen -0.225 0.0546 -4.11 3.92e- 5 -0.315 -0.135 #> 3 marMarried 0.155 0.0614 2.53 1.14e- 2 0.0545 0.256 #> 4 kid5 -0.185 0.0401 -4.61 4.08e- 6 -0.251 -0.119 #> 5 phd 0.0128 0.0264 0.486 6.27e- 1 -0.0305 0.0563 #> 6 ment 0.0255 0.00201 12.7 3.89e-37 0.0222 0.0288
在该输出中,p 值对应于每个参数的独立假设检验:
\[
\begin{align}
H_0&: \beta_j = 0 \notag \\
H_a&: \beta_j \ne 0 \notag
\end{align}
\]
对于模型中的每个参数而言。从这些结果来看,phd(即他们所在院系的声望)可能与最终结果并无关联。
虽然泊松分布通常是这类数据的常规假设,但为了更稳妥起见,我们不妨先粗略检验一下模型假设:可以不采用泊松似然函数来计算置信区间,直接拟合模型。rsample 包提供了一个便捷函数,可用于为lm() glm() family = poisson,以生成大量模型拟合结果。默认情况下,我们将计算90%的自助法的t置信区间(当然,分位数区间也可选):
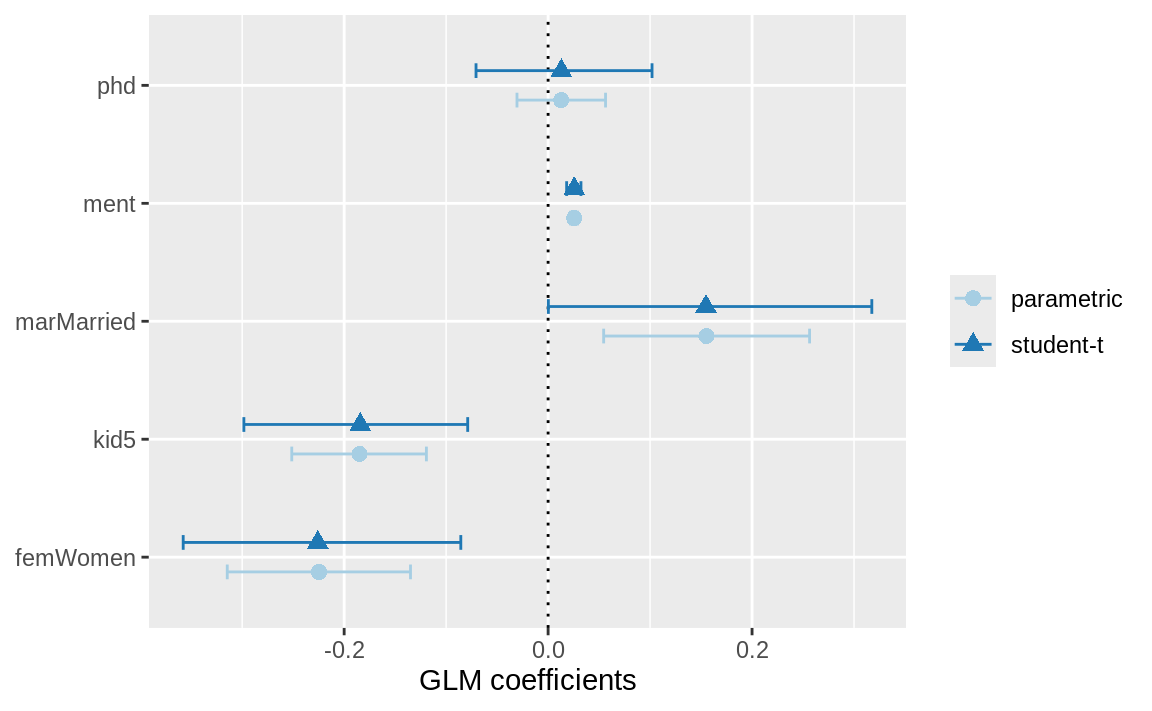
set.seed ( 2103 ) glm_boot <- reg_intervals ( art ~ . , data = bioChemists , model_fn = "glm" , family = poisson )
glm_boot #> # A tibble: 5 × 6 #> term .lower .estimate .upper .alpha .method #> <chr> <dbl> <dbl> <dbl> <dbl> <chr> #> 1 femWomen -0.358 -0.226 -0.0856 0.05 student-t #> 2 kid5 -0.298 -0.184 -0.0789 0.05 student-t #> 3 marMarried 0.000264 0.155 0.317 0.05 student-t #> 4 ment 0.0182 0.0256 0.0322 0.05 student-t #> 5 phd -0.0707 0.0130 0.102 0.05 student-t
将 Figure 4 中的这些结果与glm()
确定哪些预测变量应纳入模型是一个棘手的问题。一种方法是通过嵌套模型之间的似然比检验(LRT)(McCullagh 和 Nelder, 1989)。根据置信区间,我们有证据表明,一个不包含博士学位的简化模型可能已足够。接下来,让我们拟合一个更小的模型,然后进行统计检验:
\[
\begin{align}
H_0&: \beta_{phd} = 0 \notag \\
H_a&: \beta_{phd} \ne 0 \notag
\end{align}
\]
此前,我们已通过展示log_lin_fit的整理后结果对这一假设进行了检验。该方法采用的是单一模型拟合的结果,并借助Wald统计量(即参数除以其标准误差)来计算。结果显示,对应的p值为0.63。接下来,我们可以对似然比检验(LRT)的结果进行整理,以获得最终的p值:
log_lin_reduced <- log_lin_spec %>%
fit ( art ~ ment + kid5 + fem + mar , data = bioChemists )
anova ( extract_fit_engine ( log_lin_reduced ) ,
extract_fit_engine ( log_lin_fit ) ,
test = "LRT"
) %>% tidy ( )
#> # A tibble: 2 × 6 #> term df.residual residual.deviance df deviance p.value #> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> #> 1 art ~ ment + kid5 + f… 910 1635. NA NA NA #> 2 art ~ fem + mar + kid… 909 1634. 1 0.236 0.627
结果相同,并且根据这些结果以及该参数的置信区间,我们将不再将phd纳入后续分析,因为它似乎与研究结果无关。
A More Complex Model
我们可以在tidymodels方法中进一步探索更复杂的模型。对于计数数据,有时零值的出现频率会高于简单泊松分布所预测的水平。针对这种情况,一种更为复杂的模型是零膨胀泊松(ZIP)模型;具体可参考Mullahy(1986)、Lambert(1992)以及Zeileis、Kleiber和Jackman(2008)。在这个模型中,我们使用两组协变量:一组用于处理计数数据,另一组则影响零值的概率(记为 \(\pi\) )。均值\(\lambda\) 的计算公式如下:
\[\lambda = 0 \pi + (1 - \pi) \lambda_{nz}\]
其中:
\[
\begin{align}
\log(\lambda_{nz}) &= \beta_0 + \beta_1x_1 + \ldots + \beta_px_p \notag \\
\log\left(\frac{\pi}{1-\pi}\right) &= \gamma_0 + \gamma_1z_1 + \ldots + \gamma_qz_q \notag
\end{align}
\]
以及\(x\) 协变量影响计数值,而\(z\) 协变量则影响零概率。这两组预测变量无需彼此互斥。
我们将拟合一个包含完整一组\(z\) 协变量的模型:
zero_inflated_spec <- poisson_reg ( ) %>% set_engine ( "zeroinfl" ) zero_inflated_fit <- zero_inflated_spec %>%
fit ( art ~ fem + mar + kid5 + ment | fem + mar + kid5 + phd + ment ,
data = bioChemists
)
zero_inflated_fit #> parsnip model object #> #> #> Call: #> pscl::zeroinfl(formula = art ~ fem + mar + kid5 + ment | fem + mar + #> kid5 + phd + ment, data = data) #> #> Count model coefficients (poisson with log link): #> (Intercept) femWomen marMarried kid5 ment #> 0.62116 -0.20907 0.10505 -0.14281 0.01798 #> #> Zero-inflation model coefficients (binomial with logit link): #> (Intercept) femWomen marMarried kid5 phd #> -0.60864 0.10927 -0.35293 0.21946 0.01236 #> ment #> -0.13509
由于该模型的系数也是通过最大似然法估计的,因此我们尝试使用另一种似然比检验,以判断新模型项是否有效。我们将同时检验以下假设:
\[
\begin{align}
H_0&: \gamma_1 = 0, \gamma_2 = 0, \cdots, \gamma_5 = 0 \notag \\
H_a&: \text{at least one } \gamma \ne 0 \notag
\end{align}
\]
我们再试一次ANOVA:
zeroinfl对象未实现anova()
另一种方法是使用信息准则统计量,例如赤池信息准则(AIC)(Claeskens 2016)。该准则通过计算训练集的对数似然值,并根据训练集大小及模型参数数量对该值进行惩罚。在R语言的参数化设置中,AIC值越小越好。需要注意的是,这里我们并非进行正式的统计检验,而是评估数据拟合自身的能力。
结果表明,ZIP模型更为可取:
然而,很难将这对单一数值置于具体情境中,也难以评估它们究竟有多大的差异。为了解决这一问题,我们将对这两种模型分别进行大量重采样。通过这些重采样数据,我们可以计算出每种模型的AIC值,并确定结果有多少次倾向于ZIP模型。简而言之,我们将量化AIC统计量的不确定性,从而判断其与数据中噪声相比的差异程度。
此外,我们稍后还会计算更多基于自助法的参数置信区间,因此在生成自助样本时,需明确指定apparent = TRUE选项。这是某些类型区间所必需的设置。
首先,我们创建了4000个模型拟合:
zip_form <- art ~ fem + mar + kid5 + ment | fem + mar + kid5 + phd + ment glm_form <- art ~ fem + mar + kid5 + ment set.seed ( 2104 ) bootstrap_models <- bootstraps ( bioChemists , times = 2000 , apparent = TRUE ) %>%
mutate (
glm = map ( splits , ~ fit ( log_lin_spec , glm_form , data = analysis ( .x ) ) ) ,
zip = map ( splits , ~ fit ( zero_inflated_spec , zip_form , data = analysis ( .x ) ) )
)
bootstrap_models #> # Bootstrap sampling with apparent sample #> # A tibble: 2,001 × 4 #> splits id glm zip #> <list> <chr> <list> <list> #> 1 <split [915/355]> Bootstrap0001 <fit[+]> <fit[+]> #> 2 <split [915/333]> Bootstrap0002 <fit[+]> <fit[+]> #> 3 <split [915/337]> Bootstrap0003 <fit[+]> <fit[+]> #> 4 <split [915/344]> Bootstrap0004 <fit[+]> <fit[+]> #> 5 <split [915/351]> Bootstrap0005 <fit[+]> <fit[+]> #> 6 <split [915/354]> Bootstrap0006 <fit[+]> <fit[+]> #> # ℹ 1,995 more rows
现在,我们可以提取模型拟合结果及其对应的AIC值:
从这些结果来看,考虑过多的零计数显然是个好主意。
我们本可以使用fit_resamples()或工作流设置来执行这些计算。在本节中,我们利用mutate()和map()函数来构建模型,以展示如何针对那些未被某个parsnip包支持的模型,灵活运用tidymodels工具。
既然我们已经计算了重新采样的模型拟合结果,接下来让我们为零概率模型的系数(即 \(\gamma_j\) )创建自助法置信区间。我们可以通过tidy() type = "zero"选项来获得这些估计值:
bootstrap_models <- bootstrap_models %>%
mutate ( zero_coefs = map ( zip , ~ tidy ( .x , type = "zero" ) ) )
# One example: bootstrap_models $ zero_coefs [[ 1 ] ] #> # A tibble: 6 × 6 #> term type estimate std.error statistic p.value #> <chr> <chr> <dbl> <dbl> <dbl> <dbl> #> 1 (Intercept) zero -0.128 0.497 -0.257 0.797 #> 2 femWomen zero -0.0763 0.319 -0.240 0.811 #> 3 marMarried zero -0.112 0.365 -0.307 0.759 #> 4 kid5 zero 0.270 0.186 1.45 0.147 #> 5 phd zero -0.178 0.132 -1.35 0.177 #> 6 ment zero -0.123 0.0315 -3.91 0.0000936
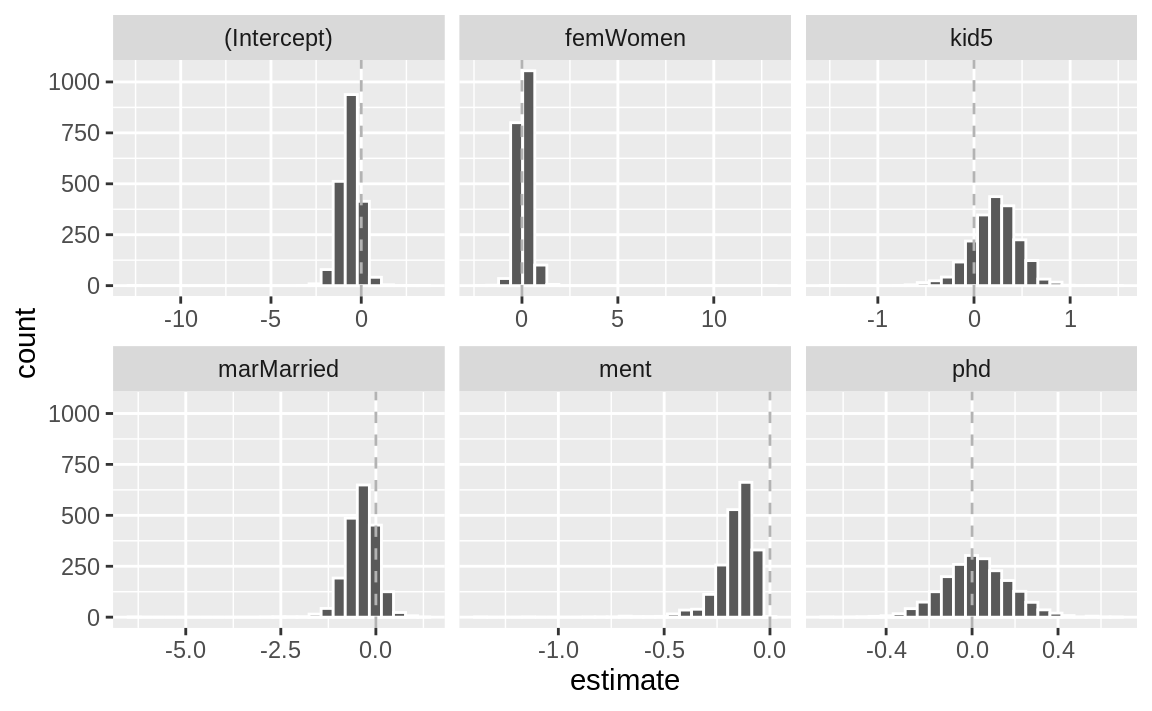
建议像 Figure 5 那样,直观地展示系数的自助分布。
bootstrap_models %>% unnest ( zero_coefs ) %>%
ggplot ( aes ( x = estimate ) ) +
geom_histogram ( bins = 25 , color = "white" ) +
facet_wrap ( ~ term , scales = "free_x" ) +
geom_vline ( xintercept = 0 , lty = 2 , color = "gray70" )
其中一个看似重要的协变量(ment)呈现出严重偏斜的分布。部分小图中出现的额外空白,表明估计值中存在一些异常值。这种情况可能发生在模型未能收敛时;因此,这些结果很可能应从重采样中剔除。而在 Figure 5 所展示的结果中,异常值仅由极端的参数估计所致;所有模型均成功收敛。
rsample 包包含一组名为int_*()的函数,用于计算不同类型的自助区间。由于tidy()
bootstrap_models %>% int_pctl ( zero_coefs ) #> # A tibble: 6 × 6 #> term .lower .estimate .upper .alpha .method #> <chr> <dbl> <dbl> <dbl> <dbl> <chr> #> 1 (Intercept) -1.76 -0.624 0.420 0.05 percentile #> 2 femWomen -0.523 0.116 0.818 0.05 percentile #> 3 kid5 -0.327 0.217 0.677 0.05 percentile #> 4 marMarried -1.20 -0.381 0.362 0.05 percentile #> 5 ment -0.401 -0.162 -0.0515 0.05 percentile #> 6 phd -0.274 0.0229 0.333 0.05 percentile bootstrap_models %>% int_t ( zero_coefs ) #> # A tibble: 6 × 6 #> term .lower .estimate .upper .alpha .method #> <chr> <dbl> <dbl> <dbl> <dbl> <chr> #> 1 (Intercept) -1.61 -0.624 0.332 0.05 student-t #> 2 femWomen -0.486 0.116 0.671 0.05 student-t #> 3 kid5 -0.211 0.217 0.599 0.05 student-t #> 4 marMarried -0.988 -0.381 0.293 0.05 student-t #> 5 ment -0.322 -0.162 -0.0275 0.05 student-t #> 6 phd -0.276 0.0229 0.291 0.05 student-t
通过这些结果,我们可以很好地了解应将哪些预测变量纳入零计数概率模型。此外,重新拟合一个更小的模型以评估ment的自助分布是否仍呈偏态,可能是明智之举。
More Inferential Analysis
本章仅展示了tidymodels中可用于推断分析的一小部分内容,重点介绍了重采样和频率学方法。不过,不可否认的是,贝叶斯分析是一种非常有效、甚至常常更优的推断方法。通过parsnip包,用户可以轻松访问多种贝叶斯模型。此外,multilevelmod包还支持用户拟合分层的贝叶斯及非贝叶斯模型(如混合效应模型)。而broom.mixed和tidybayes这两个包则是提取数据以生成图表和汇总结果的绝佳工具。最后,对于具有单一层次结构的数据集——例如简单的时间序列或重复测量数据——rsample包中的group_vfold_cv()函数能够帮助用户便捷地评估模型的样本外表现。
Chapter Summary
tidymodels 框架的应用不仅限于预测建模。通过 tidymodels 中的包和函数,不仅可以进行假设检验,还能用于拟合和评估推断模型。此外,tidymodels 框架还支持与非 tidymodels R 模型协同工作,帮助你全面评估所构建模型的统计特性。